Myron Scholes, Fischer Black, and Robert Merton: continued
Fallacies of the Nobel Gods
Scholes, Merton, and Black
The final two Nobel laureates in our group are Myron S. Scholes and Robert C. Merton, respectively of Stanford and Harvard Universities.
These two academics were honored for work in developing mathematical models for option pricing. Their output was an extension of the Capital Asset Pricing Model and was consistent with the ideas of Modern Portfolio Theory.
In 1973, Myron Scholes published a paper with Fischer Black on 'Pricing of Options and Corporate Liabilities', incorporating suggestions from Merton Miller (of M&M Theory fame) and Eugene Fama (father of the Efficient Market Hypothesis).
Black, like many other orthodox economists, was an admirer of Irving Fisher, the Yale professor sometimes cited as the greatest American economist, who lost a fortune after declaring stocks were under-valued in October 1929.
Black had a PhD in applied mathematics from Harvard and worked at Arthur D. Little, the renowned consulting firm. He later was on the faculty at the University of Chicago and MIT.
Also in 1973, Robert C. Merton, a finance professor at Harvard, was drafting a paper that improved on the Black-Scholes Model. Merton, a disciple of another Nobel laureate, Paul Samuelson, had already gained fame in academic circles for developing a theory of 'continuous time finance' which assumed that financial market prices varied in infinitesimally small steps.
The Commercialization of Math
Black and Scholes had solved stochastic partial differential equations to develop a formula for pricing European-type call options.
The result was an equation that suggested how the price of a call option might be calculated as a function of a risk-free interest rate, the price variance of the asset on which the option was written, and the parameters of the option (strike price, term, and the market price of the underlying asset.)
Fisher Black would probably have won a Nobel Prize along with Myron Scholes for this work, but he died in 1995, two years before the award.
This formula, which came to be called the Black-Scholes Model, was enormously popular.
In part this was because the Chicago Board Options Exchange had just begun trading in standardized stock options in the year the Black-Scholes Formula was published.
Also, inexpensive hand-held calculators made by Texas Instruments and Hewlett Packard could now easily handle the Black-Scholes Formula, putting the supposed power of abstruse mathematics in traders' pockets.
Financial options are promoted as insurance against variations in security prices. Just as the purchaser of life insurance does not need to check the accuracy of actuarial calculations of the insurer, option purchasers can rely on commonsense to determine if put or call options are reasonably priced for their particular needs.
On the other hand, the writer of options – the insurer – needs to have a precise grasp of the risk insured in order to stay in the option writing business for long. In this way, the Black-Scholes Model – with its many variations and competing theories – filled a need.
The Growth of Derivatives
The expansion of the trading market for financial derivatives was primarily the result of a highly efficient trading, clearing and settlement system devised by the Chicago Exchanges.
However, the Black-Scholes Model played a part by providing a tool for writers of options.
On February 20, 2020, at the very peak of the Great Bubble, the Public Broadcasting System aired a program on 'The Formula the Shook the World', describing the Black-Scholes Model as 'a mathematical Holy Grail that forever altered the world of finance' and cited an economist who 'likened the impact of the discovery of the Black-Scholes Formula to that of the discovery of the structure of DNA.'
(NOVA Online web site, produced February 2000 by WGBH Science Unit for PBS.)
This, of course, was ridiculous hyperbole, since there was nothing scientific about the Black-Scholes Model and the likelihood of its 'forever altering the world of finance' had already been severely curtailed when the formula's weaknesses were spectacularly demonstrated in 1998 with the multi-billion dollar implosion of Long Term Capital Management.
The Black-Scholes Fantasy
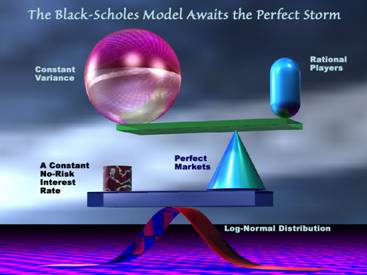
Like the work of the other Nobel laureate economists that played a part in the Great Bubble of the 1990s, the Black-Scholes Model was laced with unrealistic assumptions and fatal flaws:
Perfect Markets. The markets were presumed to be extremely deep so that traders' actions could not affect prices.
This assumption ignored actual market conditions in the early days of the Chicago Board Options Exchange, the role of option traders in the Crash of 1987, and OTC market illiquidity which helped to bring down Long Term Capital Management – of which Scholes and Merton were partners – in 1998.
No-Risk Operations, Continuous Pricing, Perfect Order Execution. Organized securities exchanges do not have continuous pricing, but trade in discreet jumps called 'ticks'.
As prices fall, these 'ticks' become proportionately larger. All markets have operational risks and order execution is never perfect.
Rational Market Players that React Immediately to News. By 'rational behavior', the theorists meant that all market players would react so as to maximize returns and minimize losses, presumably using the Black-Scholes formula as a basis.
Price Variations Following a Log-Normal (Gaussian) Distribution. If this were true, extreme price fluctuations would almost never be observed. For example, the Crash of 1987 would not have occurred if price fluctuations truly followed the log-normal pattern.
Furthermore, the price variation of each trade would be random and independent of the previous trade. There could be no panic selling or mob buying. Prices would have an equal chance of rising or falling – although historical data over the longer term has shown that prices drift upwards.
A Constant, Risk-Free Interest Rate Available as a Benchmark. The interest rate on short-term U.S. Treasury bills was generally assumed to represent the risk-free rate needed by the model.
However, this rate is never constant. Furthermore, options markets are international and the stability of the U.S. Treasury rate is not the same to a German thinking in terms of Euros, or to a Japanese measuring rate changes in Yen.
Volatility in Stock Prices that is Constant during the Life of an Option. In real markets, stock volatility is never constant. Without a constant volatility factor, the Black-Scholes Model does not work.
A World made up of Risk-free Counterparties and Legal Certainty. Even if governments were the counterparty to each trade, there would be counterpart risk. Clearing and settlement of securities transactions is mined with legal traps that spring at the wrong time.
The Black-Scholes Model implicitly assumed that operations of U.S. financial markets were universal. However, it would be folly to use the formula to trade options in a Third World country with high inflation, teetering government, and shaky currency.
Although the composition of DNA may be the same in Tanzania as in New York, the same scientific universality does not apply to the Black-Scholes formula.
Long Term Capital Management and the Perfect Storm
The numerous flaws in the Black-Scholes Model meant that anyone who took the formula too seriously – especially using it as a basis for highly leveraged trades – would be betting on an extremely unstable structure.
Particularly scary conditions result when one assumes log-normal distribution of price variations in a world in which prices often moved beyond the confines of the log-normal curve.
These 'out-rider' fluctuations – so-called 'fat-tails' of the distribution curve – occurred in the Crash of 1987 and in various debacles in emerging markets in the 1980s and 1990s.
One such supposedly 'hundred-year event' – a Perfect Storm – brought down Long Term Capital Management in 1998, along with the pride of the Nobel laureates Scholes and Merton who were participants in the fiasco.
In other words, the discovery of the Black-Scholes Model instead of being the financial equivalent of a great discovery in physics or medicine was a non-scientific calamity waiting to happen.
Power to Cloud Men's Minds
As capital flow analysts, we are less concerned with the rise and fall of the reputation of a handful of Nobel laureates than we are of the impact of their teachings on the sociology of the broader securities markets.
In general, these six Nobel laureates led a much larger cohort of market experts who argued that capital gains were as good as dividends, that market risks could be managed, that debt was just as good as equity, and that the proper aim of equity investment should be year-to-year total return.
These heresies against the conservative banking practices of the 1950s and the thinking of investors in the now distant past, like Benjamin Graham and John Burr Williams, led to perilous over-extensions in the financial system and a generalized substitution of long-term investment by short-term speculation and undisguised gambling.
A fog of higher mathematics and surreal assumptions rolled over older concepts of value, roiling greedy impulses that ruled the Great Bubble and hindered awareness that rising stock prices might be the result of scarcity, rather than greater worth, as was presumed.
The unrelenting persistence of this misapprehension was fomented by institutionalized teaching of doctrines of the Nobel gods. The Great Bubble was not a temporary hysteria or madness, fanned by a cult leader in the jungles of South America or at an armed compound on the outskirts of Waco, Texas.
Instead, the canons of the Nobel gods were laced into the intellectual Kool-Aid served to youngsters seeking MBAs at the Great Universities, thereby providing an army of Lesser Fools as the next generation of investors and professional corporate managers.
Such new-age financial thinking became an essential element in evolving perceptions of risk and was instrumental in creating a global, hundred-trillion dollar derivatives market.
The counterparties to Lesser Fool investors were the risk-loving corporate managers, addicted to the 'asset-lite' methods of the Nobel gods that further curtailed the supply of equities.
In other essays, I examine how the fallacies of the 'asset-lite' movement pushed financial markets to new levels of instability, triggering the Enron and WorldCom bankruptcies and casting long, dark shadows on the banking system of the twenty-first century.